How Do You Know When a Radical Function Crosses the Horizontal Asymptote Purple Math

Horizontal Asymptotes

Whereas vertical asymptotes are sacred ground, horizontal asymptotes are just useful suggestions.

Whereas you can never touch a vertical asymptote, you lot can (and oft do) touch and even cross horizontal asymptotes.

Whereas vertical asymptotes indicate very specific behavior (on the graph), normally close to the origin, horizontal asymptotes indicate general beliefs, normally far off to the sides of the graph.

In other words, horizontal asymptotes are different from vertical asymptotes in some fairly significant ways.

Content Continues Below

To empathise the concept of horizontal asymptotes, let'southward look at a few examples.

• Find the horizontal asymptote of the post-obit office:

Starting time, notice that the denominator is a sum of squares, and then information technology doesn't gene and has no real zeroes. In other words, this rational function has no vertical asymptotes. Then we're okay on that front.

As mentioned above, the horizontal asymptote of a function (bold it has one) tells me roughly where the graph will being going when ten gets really, actually big. So I'll wait at some very big values for 10 ; that is, at some values of x which are very far from the origin:

Off to the sides of the graph, where 10 is strongly negative (such every bit −1,000) or else strongly positive (such every bit 10000) the "+two" and the "+ane" in the expression for y really don't thing and then much. I concluded up having a really large number divided past a actually big number squared, which "simplified" to be a very small number. The values of y came mostly from the " ten " and the " x ² ", especially once x got very large. And since the x ^two was "bigger" than the x , the x ² dragged the value of the whole fraction down to y = 0 (that is, down to the ten -centrality) when 10 got big.

This makes perfect sense, when you think about it. If you've got a zillion (plus two, but who cares most that?) divided past a zillion squared (plus 1, but who cares about that?), then you've essentially got a zillion divided by the foursquare of a zillion, which simplifies to 1 over a zillion. Which is very, very small. So of course the value of the function gets very, very small; namely, it gets very, very close to cypher.

I tin see this behavior on the graph, if I zoom out on the x -axis:

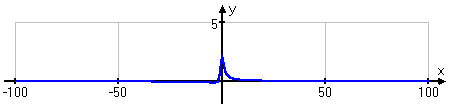
The graph shows that there's some slightly interesting behavior in the heart, right near the origin, simply the rest of the graph is fairly boring, abaft along the 10 -axis.

If I zoom in on the origin, I tin likewise see that the graph crosses the horizontal asymptote (at the arrow):

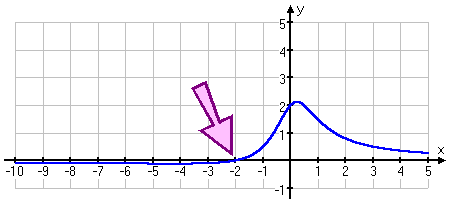
It is common and perfectly okay to cantankerous a horizontal asymptote. (Information technology's the vertical asymptotes that I'one thousand not allowed to bear on.)

As I can come across in the tabular array of values and the graph, the horizontal asymptote is the x -axis.

horizontal asymptote: y = 0 (the 10 -centrality)

In the above exercise, the degree on the denominator (namely, 2) was bigger than the degree on the numerator (namely, 1), and the horizontal asymptote was y = 0 (the x -axis). This property is ever truthful: If the degree on ten in the denominator is larger than the degree on x in the numerator, then the denominator, existence "stronger", pulls the fraction down to the x -axis when x gets large. That is, if the polynomial in the denominator has a bigger leading exponent than the polynomial in the numerator, and so the graph trails forth the x -axis at the far correct and the far left of the graph. And then any fourth dimension the power on the denominator is larger than the power on the numerator, the horizontal asymptote is going to be the the 10 -centrality, also known as the line y = 0.

---

What happens if the degrees are the aforementioned in the numerator and denominator? Let's take a look:

• Find the horizontal asymptote of the following:

Unlike the previous instance, this role has degree-2 polynomials top and bottom; in detail, the degrees are the same in the numerator and the denominator. Since the degrees are the same, the numerator and denominator "pull" evenly; this graph should not drag down to the x -axis, nor should it shoot off to infinity. Merely where will it go?

Again, I need to recollect in terms of big values for x . When 10 is actually large, I'll have, roughly, twice something big (minus an eleven, but who cares about that?) divided past one time something big (plus a ix, simply who cares nearly that?).

Every bit you might judge from the last do, the "–xi" and the "+9" won't matter much for actually big values of x . Far off to the sides of the graph, I'll roughly take , which reduces to just 2.

Does a table of values conduct this out? Let's check:

For big values of x , the value of the role is, every bit expected, very close to y = two. And the graph of the function reflects this:

Sure, there's probably something interesting going on in the centre of the graph, near the origin. But, off to the sides, the graph is conspicuously sticking very shut to the line y = two. (In calculus, you'll learn how to prove this yourself.)

And then my reply is:

horizontal asymptote: y = 2

In the example above, the degrees on the numerator and denominator were the same, and the horizontal asymptote turned out to be the horizontal line whose y -value was equal to the value found by dividing the leading coefficients of the ii polynomials. This is always true: When the degrees of the numerator and the denominator are the same, and so the horizontal asymptote is found by dividing the leading terms, so the asymptote is given by:

y = (numerator'south leading coefficient) / (denominator'south leading coefficient)

---

• Notice the horizontal asymptote of .

Now that I know the rules well-nigh the powers, I don't accept to do a table of values or draw the graph. I tin can just compare exponents.

In this rational function, the highest power in each of the numerator and the denominator is the same; namely, the cube.

(This fraction might feel a petty bit misleading, because the highest-power term in the denominator is non the showtime term. But that's okay; all I need to discover is whichever term has the largest exponent. It doesn't thing where, within the expression, that term is located.)

So I know that this role's graph will have a horizontal asymptote which is the value of the division of the coefficients of the terms with the highest powers. Those coefficients are 4 and −3. Then my answer is:

hor. asymp.:

---

• Find the horizontal asymptote of

The highest power in the numerator is two. In that location is an 10 ² in the denominator, simply that doesn't matter, considering the highest power in the denominator is five.

Since the largest power underneath is bigger than the largest power on superlative, and then the horizontal asymptote will be the horizontal axis.

hor. asymp.: y = 0

harrisonpubt1973.blogspot.com

Source: https://www.purplemath.com/modules/asymtote2.htm